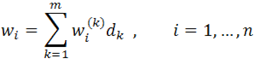Analytical Hierachy Process przedstawiona przez Thomasa L Saaty’ego [18]– technika modelowania i oceny problemów decyzyjnych, dostępnych opcji działania, w celu wsparcia podejmowania decyzji. Ułatwia wybór rozwiązania na podstawie oceny według wybranych kryteriów, biorąc od uwagę preferencje oceniającego.
Jest techniką ocen parametrów z wykorzystaniem bezwzględnej skali (dla kryteriów mierzalnych i niemierzalnych).
Metoda polega na dekompozycji problemu na elementy składowe i powtarzanie sekwencji ocen na zasadzie porównywania elementów parami.
Problem decyzyjny jest modelowany w postaci drzewa, gdzie poziom pierwszy przedstawia ogólny cel, poziomy kolejne zawierają kryteria i podkryteria oceny, a poziom najniższy zawiera dostępne opcje, alternatywne działania, decyzje.
W celu określenia wagi poszczególnych kryteriów, są one porównywane parami (ang. pair-wise comparisons) przy użyciu skali zaproponowanej przez Saaty-ego [28]:
| 1 | Elementy równoważne |
| 3 | Umiarkowana preferencja i nad j |
| 5 | Silna preferencja i nad j |
| 7 | Bardzo silna preferencja i nad j |
| 9 | Zdecydowana, krytyczna preferencja i nad j |
| 2, 4, 6, 8 | Możliwe wartości pośrednie |
| 1/2, 1/3, 1/4, …, 1/9 | Odwrotności powyższych wartości oznaczają preferencję elementu j nad i |
Decydenci wyrażają swoje preferencje za pomocą powyższej skali a wynik porównań jest zapisywany w postaci kwadratowej macierzy preferencji. Powstała macierz jest macierzą kwadratową, o wymiarze równym liczbie porównywanych elementów.
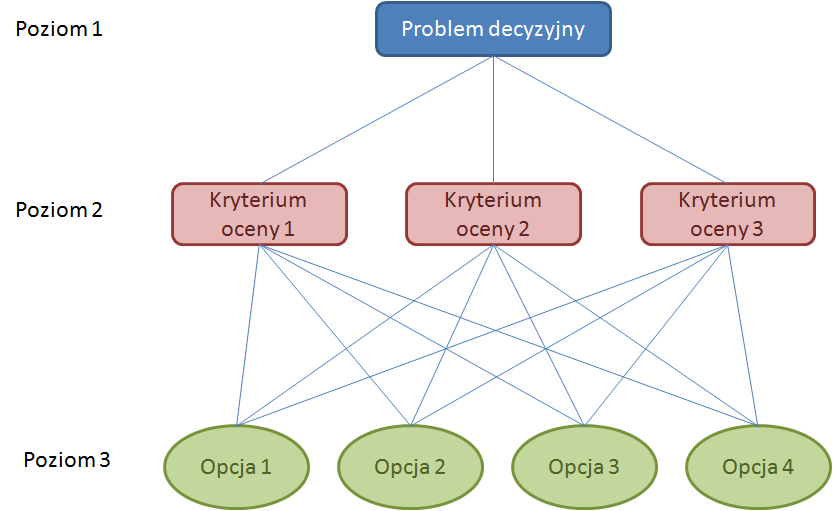
Dla każdego nadrzędnego kryterium oceny Kk (posiadającego elementy potomne), powstaje matryca oceny:
Ak={aij},
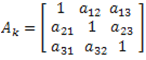
gdzie aij jest wartością, która mówi o ile ważniejszy jest element i od elementu j w odniesieniu do Kk.
Powstała macierz oceny jest proporcjonalną, czyli elementy macierzy spełniają zależność
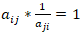
czyli
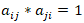
gdzie 
.
Tzn. jeżeli wagę kryterium K1 względem K3 oceniono na 5 (a13 = 5), to wartość porównania odwrotnego – K3 względem K1, powinna być odwrotnością wcześniejszej oceny (a31 = 1/5).
Jeżeli dodatkowo zachodzą zależności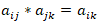 
, to matryca jest spójna.
Na powyższym przykładzie:
a12*a23=a13
2 * 5/2 = 5,
więc matryca jest spójna. W praktyce takie matryce występują rzadko. Przyjęta skala oceny przy użyciu zbioru wartości Z = {1/9, 1/8, …, 1/2, 1, 2, …, 8, 9} również nie przyczynia się do zachowanie spójności matrycy (w przykładowej matrycy wartości 2/5, 5/2 nie należ do zbioru Z).
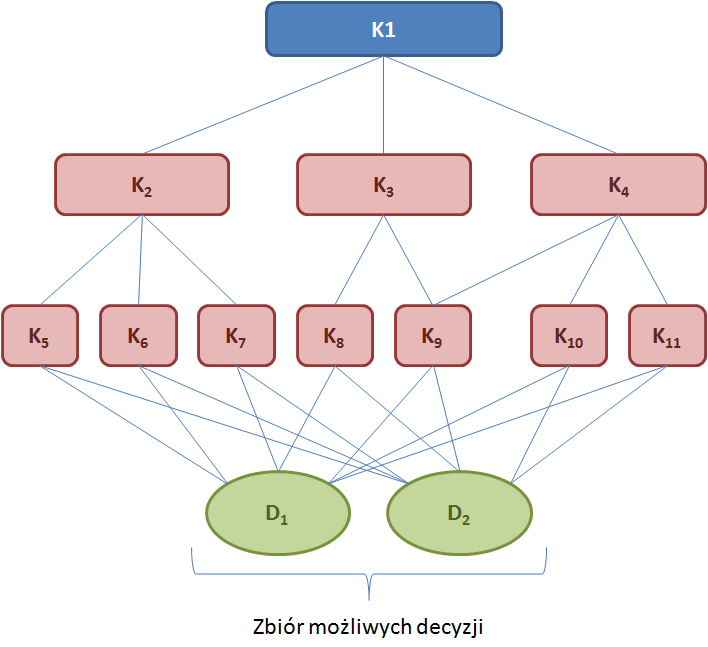
Poniżej przedstawiono graf przykładowego schematu decyzyjnego, dla którego można rozważyć przykładową ocenę kryteriów (K1, K2, K3), przedstawioną w poniższej tabeli.
Przykład na podstawie [19].
| Element matrycy (aij) | ai1 | ai2 | ai3 | |
| Porównywane kryteria | K2 | K3 | K4 | |
| a1j | K2 | 1 | 6 | 8 |
| a2j | K3 | 1/6 | 1 | 4 |
| a3j | K4 | 1/8 | 1/4 | 1 |
Tabela 1. Przykład tabeli z ocenami porównań kryteriów.
Kolejnym krokiem w metodzie AHP jest obliczenie wektora własnego macierzy preferencji.
Stosowane są różne metody przybliżonego obliczania wektora własnego macierzy porównań. Sam autor, Thomas Saaty proponuje kilka metod. Poniżej przedstawiono dwie główne [20], [22]:
Metoda I (Saaty’ego)
Przykłady na podstawie [21]
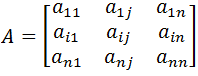
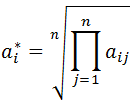
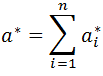
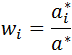
Przykład:
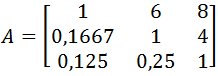
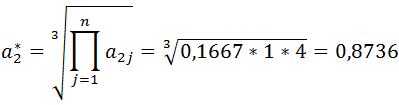
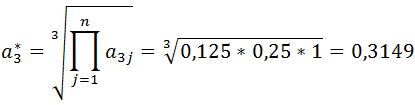
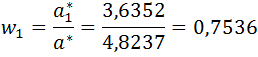
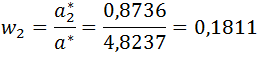
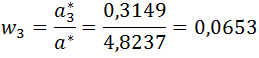
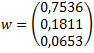
Metoda II (Saaty’ego)
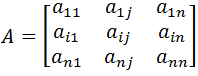
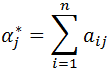
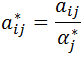
Przykład:
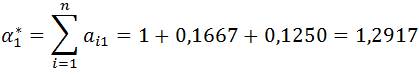
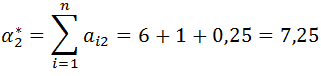
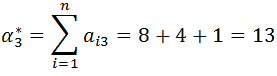
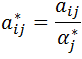
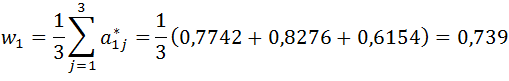
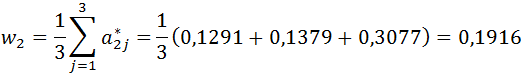
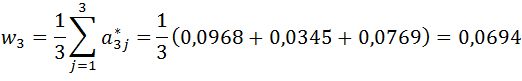
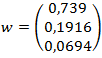
Inne metody
Ponadto stosowane są inne uproszczone podejścia [19], polegające na obliczeniu przybliżonych wartości wektora rozkładów priorytetów z pierwotnej postaci macierzy preferencji. Dla przeprowadzonych porównań parami obliczane są sumy poszczególnych wierszy matrycy, a następnie wartości te są dzielone przez ich sumę (normalizowanie do jedności):
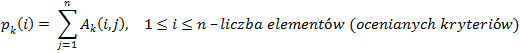
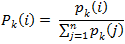
Dla macierzy z wcześniejszego przykładu wektor rozkładu priorytetów (przedstawiany dalej jako wektor kolumnowy, w formie macierzy) jest obliczany następująco:
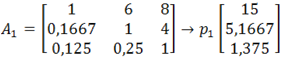
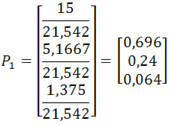
Wartości macierzy p1 są sumami poszczególnych wierszy macierzy A1. Dzieląc kolejne wartości p1 przez sumę wartości p1, otrzymujemy wektor priorytetów dla kryteriów K2, K3, K4 (wartości w macierzy P1 są znormalizowane do jedności).
Następnie w ten sam sposób wyznaczane są priorytety podkryteriów (K5, …, K11) każdego z kryteriów nadrzędnych (K2, K3, K4). Tzn. dla kryterium K2 oceniane (porównywane parami) są podkryteria K5, K6, K7, dla kryterium K3 porównywane są podkryteria K8 i K9, a dla kryterium K4, podkryteria K9, K10, K11.
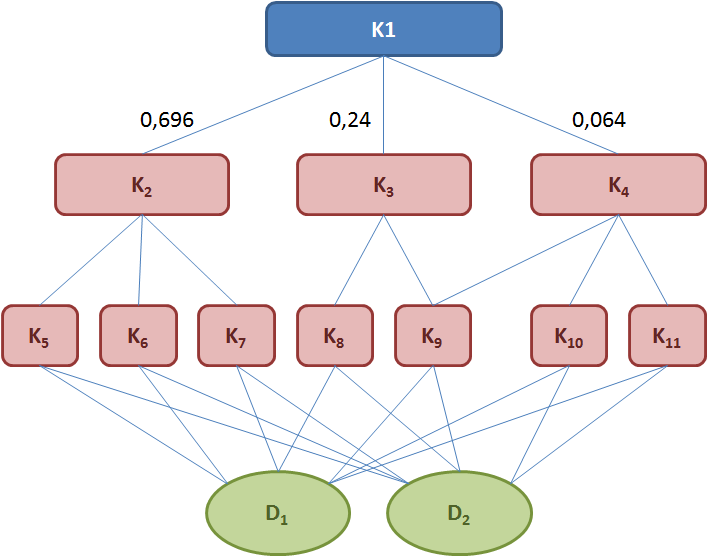
Dla kryterium K2 powstanie więc macierz wyników porównań (A2), o wartościach np. jak w poniższej tabeli:
| Element matrycy (aij) | ai1 | ai2 | ai3 | |
| Porównywane kryteria | K5 | K6 | K7 | |
| a1j | K5 | 1 | 1/3 | 2 |
| a2j | K6 | 3 | 1 | 4 |
| a3j | K7 | 1/2 | 1/4 | 1 |
Na tej podstawie można wyznaczyć macierz priorytetów:
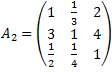
W ten sam sposób można wyznaczyć priorytety dla kolejnych kryteriów.
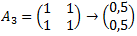
Ostatecznie otrzymamy wartości jak na poniższym grafie.
—-
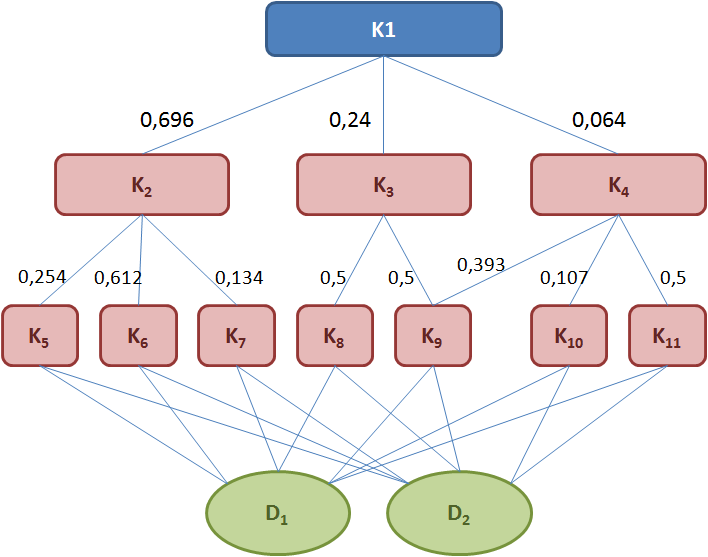
Kolejnym etapem w klasycznym podejściu do AHP, jest utworzenie macierzy porównań każdej z opcji, względem każdego z kryteriów ostatniego poziomu. W powyższym przykładzie będzie to 7 macierzy porównań (dla każdego z kryteriów K5, …, K11) o rozmiarze 2×2 (dwie oceniane opcje – D1, D2). Poniżej przedstawiono macierze wynikowe oceny (porównania) opcji. Do obliczenia wektora priorytetów została użyta uproszczona metoda normalizowania do jedności (patrz opis w sekcji „Inne metody”):
- porównanie względem kryterium K5:
| D1 | 1 | 2 |
|---|---|---|
| D2 | 1/2 | 1 |
- porównanie względem kryterium K6:
| D1 | 1 | 5 |
|---|---|---|
| D2 | 1/5 | 1 |
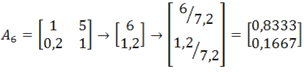
- porównanie względem kryterium K7:
| D1 | 1 | 1/9 |
|---|---|---|
| D2 | 9 | 1 |
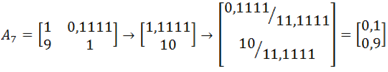
- porównanie względem kryterium K8:
| D1 | 1 | 8 |
|---|---|---|
| D2 | 1/8 | 1 |
- porównanie względem kryterium K9:
| D1 | 1 | 1 |
|---|---|---|
| D2 | 1 | 1 |
- porównanie względem kryterium K10:
| D1 | 1 | 1/2 |
|---|---|---|
| D2 | 2 | 1 |
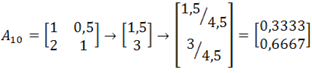
- porównanie względem kryterium K11:
| D1 | 1 | 1/3 |
|---|---|---|
| D2 | 3 | 1 |
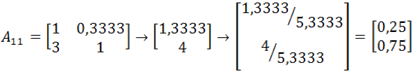
Ostatecznie, dla przykładowego grafu wartości poszczególnych porównań rozkładają się następująco:
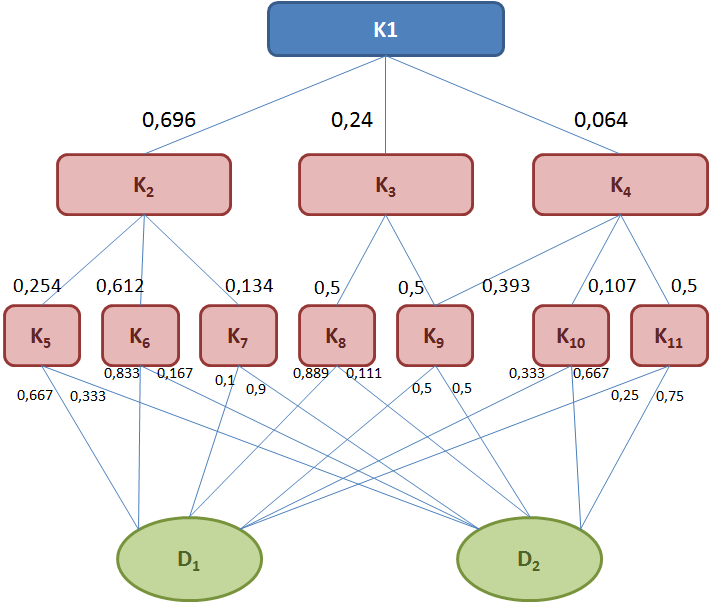
Globalne priorytety dla opcji D1 i D2 można obliczyć jako sumy iloczynów priorytetów w każdej gałęzi, od opcji aż do celu głównego.
P1= 0,667*0,254*0,696 + 0,833*0,612*0,696 + 0,1*0,134*0,696 + 0,889*0,5*0,24 + 0,5*0,5*0,24 + 0,05*0,393*0,064 + 0,333*0,107*0,064 + 0,25*0,5*0,064 =
= 0,1179 + 0,3761 + 0,0093 + 0,1067 + 0,0600 + 0,0126 + 0,0023 + 0,0080 =
= 0,6929
P2= 0,333*0,254*0,696 + 0,167*0,612*0,696 + 0,9*0,134*0,696 + 0,111*0,5*0,24 + 0,5*0,5*0,24 + 0,05*0,393*0,064 + 0,667*0,107*0,064 + 0,75*0,5*0,064 =
= 0,0589 + 0,0711 + 0,0839 + 0,0133 + 0,0600 + 0,0126 + 0,0046 + 0,0240 =
= 0,3284
Wyżej ocenianą opcją jest więc D1.
Badanie spójności ocen
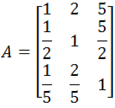
Powyższa macierz przedstawiona już wcześnie w tym rozdziale prezentuje oceny spójne (cechy spójności przedstawiono wcześniej). Jednak ze względu na to, że oceny w ramach AHP są wydawane z wykorzystaniem ustalonej, stałej skali wartości (bez wartości pośrednich) oraz biorąc pod uwagę, że zawierają one subiektywne preferencje oceniających, praktycznie niemożliwe jest uzyskanie spójnych macierzy porównań. Możliwa jest jednak ocena poziomu spójności, a przez to również przyjęcie pewnego akceptowalnego poziomu spójności.
W celu zapewnienia lepszej jakości wyników, pierwotna metoda AHP proponuje obliczenie współczynnika spójności (CR – Consistency Ratio), który jest wyznaczany jako stosunek indeksu spójności (CI – Consistency Index) macierzy porównań parami, do indeksu spójności przypadkowych wartości macierzy tego samego rozmiaru (RI – Random Index).
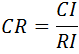
Indeks zgodności (CI – Consistency Index) macierzy obliczany jest wg wzoru:
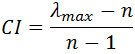
gdzie n to rozmiar macierzy, natomiast λmax to największa wartość własna macierzy.
RI to indeks spójności macierzy, której wartości są całkowicie przypadkowe.
Poniżej przedstawione tabele typowych, stosowanych wartości RI dla macierzy o rozmiarze n od 1 do 15
Przykład 1 [18] – RI wyznaczony na podstawie 100 symulacji
| RI | 0 | 0 | 0,382 | 0,946 | 1,220 | 1,032 | 1,468 | 1,402 | 1,350 | 1,464 | 1,576 | 1,476 | 1,564 | 1,568 | 1,586 |
Przykład 2 [23] – RI wyznaczony na podstawie 1000 symulacji
| RI | 0 | 0 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 | 1,51 | 1,48 | 1,56 | 1,57 | 1,59 |
Przykład 3 [24] – RI wyznaczony na podstawie 100000 symulacji
| RI | 0 | 0 | 0,5245 | 0,8815 | 1,1086 | 1,2479 | 1,3417 | 1,4056 | 1,4499 | 1,4854 | 1,5141 | 1,5365 | 1,5551 | 1,5713 | 1,5838 |
Wyznaczanie wartości własnej macierzy
Według metody Saaty’ego, wartość własna λmax może być wyznaczona ze wzoru:
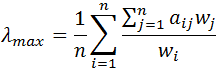
Stąd dla rozważanej wcześniej macierzy:
| Element matrycy (aij) | ai1 | ai2 | ai3 | |
| Porównywane kryteria | K2 | K3 | K4 | |
| a1j | K2 | 1 | 6 | 8 |
| a2j | K3 | 1/6 | 1 | 4 |
| a3j | K4 | 1/8 | 1/4 | 1 |
wektor własny można wyznaczyć następująco:
- wektor w został wyznaczony za pomocą I metody Saaty’ego (opisanej wcześniej),
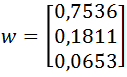
- następnie wartości z każdej komórki aij są mnożone przez wartość j tego wektora (aij*wj):
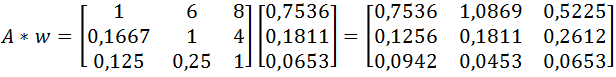
- wartości w wierszach macierzy wynikowej są sumowane i otrzymujemy wektor:
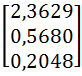
- otrzymane wartości dzielimy przez wartości wektora w
- wartość λmax wyznaczamy jako średnią wartości wektora wynikowego
λmax = 3,135657
Dla tak wyznaczonej wartości własnej możliwe jest obliczenie indeksu spójności:
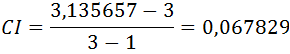
Z kolei wartość współczynnika spójności obliczamy stosując wartość z tablicy spójności przypadkowych (Random Index). Np. stosując wartości wyznaczone przez Goldena i Wanga [23], dla macierzy o n=3, index RI=0,58.
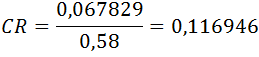
Ocenę zwykle uznaje się za zadowalającą, jeżeli współczynnik zgodności CR < 0,1.
Agregowanie ocen
Źródła: [25], [26]
Oceny alternatyw i kryteriów mogą być prowadzone razem a wartości wynikowe (uzgodnione w grupie) będą wprowadzane w macierzach porównań parami. Jednak oceny mogą być również prowadzone przez kilka osób oddzielnie, niezależnie. Dlatego kolejnym problemem w metodach wielokryterialnych (jak AHP) jest agregowanie ocen wykonywanych przez różne osoby.
Poszczególne osoby prowadzące ocenę, porównania kryteriów i opcji, mają różne poglądy, priorytety. Stosowane są różne podejścia do agregacji indywidualnych ocen, w celu uzyskania wspólnego wyniku, jak:
- agregowanie każdej z ocen w trakcie (porównań) parami,
- synteza wyników dla każdej osoby (ustalenie jej hierarchii, priorytetów) a następnie zagregowanie wynikowych priorytetów,
- agregowanie priorytetów wyznaczonych na poszczególnych poziomach hierarchii, dla poszczególnych węzłów drzewa decyzyjnego.
W najprostszej postacji agregacja może być wykonana jako średnia geometryczna lub arytmetyczna.
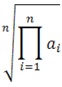
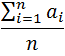
Przy obliczaniu zagregowanych wartości często zakłada się równą wagę ocen wykonanych przez poszczególne osoby. W praktyce, przy podejmowaniu decyzji, wyższą wagę będą miały oceny i głosy osób ostatecznie podejmujących decyzję. Wyniki ocen będą więc miały różną wagę podczas agregacji wyników.
Do agregacji pojedynczych ocen w macierzach porównań stosuje się głównie metodę średniej geometrycznej ważonej. Wówczas poszczególne wartości dla zagregowanej macierzy porównań parami wyznacza się jako:
gdzie:
aij jest wynikiem pojedynczego porównania (element macierzy porównań),
m jest liczbą oceniających,
dk to miary ważności oceniającego (wagi oceniających), określone w taki, że suma wag wszystkich oceniających =1:
W przypadku agregacji wyników dla priorytetów (wektorów macierzy ocen) określonych przez poszczególne osoby, zwykle stosuje się średnią arytmetyczną ważoną. Wówczas wektory macierzy pojedynczych ocen agreguje się do wspólnego wektora priorytetów dla grupy oceniających w=(w1, …, wn), zgodnie ze wzorem:
